 This is perhaps the first real crack in the wall for the almost-universal use of the null hypothesis significance testing procedure (NHSTP). The journal, Basic and Applied Social Psychology (BASP), has banned the use of NHSTP and related statistical procedures from their journal. They previously had stated that use of these statistical methods was no longer required but can be optional included. Now they have proceeded to a full ban.
This is perhaps the first real crack in the wall for the almost-universal use of the null hypothesis significance testing procedure (NHSTP). The journal, Basic and Applied Social Psychology (BASP), has banned the use of NHSTP and related statistical procedures from their journal. They previously had stated that use of these statistical methods was no longer required but can be optional included. Now they have proceeded to a full ban.
The type of analysis being banned is often called a frequentist analysis, and we have been highly critical in the pages of SBM of overreliance on such methods. This is the iconic p-value where <0.05 is generally considered to be statistically significant.
The process of hypothesis testing and rigorous statistical methods for doing so were worked out in the 1920s. Ronald Fisher developed the statistical methods, while Jerzy Neyman and Egon Pearson developed the process of hypothesis testing. They certainly deserve a great deal of credit for their role in crafting modern scientific procedures and making them far more quantitative and rigorous.
However, the p-value was never meant to be the sole measure of whether or not a particular hypothesis is true. Rather it was meant only as a measure of whether or not the data should be taken seriously. Further, the p-value is widely misunderstood. The precise definition is:
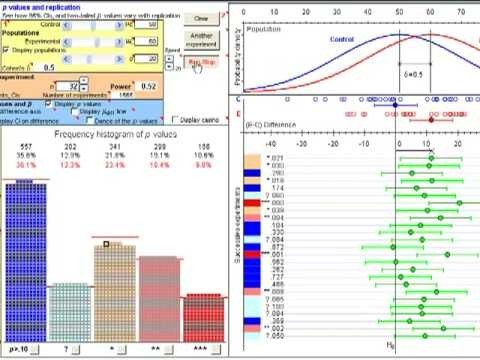
The p value is the probability to obtain an effect equal to or more extreme than the one observed presuming the null hypothesis of no effect is true.
In other words, it is the probability of the data given the null hypothesis. However, it is often misunderstood to be the probability of the hypothesis given the data. The editors understand that the journey from data to hypothesis is a statistical inference, and one that in practice has turned out to be more misleading than informative. It encourages lazy thinking – if you reach the magical p-value then your hypothesis is true. They write:
In the NHSTP, the problem is in traversing the distance from the probability of the finding, given the null hypothesis, to the probability of the null hypothesis, given the finding. Regarding confidence intervals, the problem is that, for example, a 95% confidence interval does not indicate that the parameter of interest has a 95% probability of being within the interval. Rather, it means merely that if an infinite number of samples were taken and confidence intervals computed, 95% of the confidence intervals would capture the population parameter. Analogous to how the NHSTP fails to provide the probability of the null hypothesis, which is needed to provide a strong case for rejecting it, confidence intervals do not provide a strong case for concluding that the population parameter of interest is likely to be within the stated interval.
Another problem with the p-value is that it is not highly replicable. This is demonstrated nicely by Geoff Cumming as illustrated with a video. He shows, using computer simulation, that if one study achieves a p-value of 0.05, this does not predict that an exact replication will also yield the same p-value. Using the p-value as the final arbiter of whether or not to accept or reject the null hypothesis is therefore highly unreliable.
Cumming calls this the “dance of the p-value,” because, as you can see in his video, when you repeat a virtual experiment with a phenomenon of known size, the p-values that result from the data collection dance all over the place.
Regina Nuzzo, writing in Nature in 2014, echoes these concerns. She points out that if an experiment results in a p-value of 0.01, the probability of an exact replication also achieving a p-value of 0.01 (this all assumes perfect methodology and no cheating) is 50%, not 99% as many might falsely assume.
The real world problem is worse than these pure statistics would suggest, because of a phenomenon known as p-hacking. In 2011 Simmons et al. published a paper in Psychological Science in which they demonstrate that exploiting common researcher degrees of freedom could easily manipulate the data (even innocently) to achieve the threshold p-value of 0.05. They point out that published p-values cluster suspiciously around this 0.05 level, suggesting that some degree of p-hacking is going on.
This is also often described as torturing the data until it confesses. In a 2009 systematic review, 33.7% of scientists surveyed admitted to engaging in questionable research practices – such as those that result in p-hacking. The temptation is simply too great, and the rationalizations too easy – I’ll just keep collecting data until it wanders randomly over the 0.05 p-value level, and then stop. One might argue that overreliance on the p-value as a gold standard of what is publishable encourages p-hacking.
So what’s the alternative? Many authors here have suggested either doing away with the p-value, or (a less radical solution) simply bring it back down to its proper role – it provides one measure of the robustness of the data, but is not the final arbiter of whether or not the null hypothesis should be rejected. We have also supported those researchers who have called for increased use of Bayesian analysis as a more appropriate alternative. The Bayesian approach is to ask the right question, what is the probability of the hypothesis given both the prior probability and the new data?
The BASP give a lukewarm acceptance of the Bayesian approach:
Bayesian procedures are more interesting. The usual problem with Bayesian procedures is that they depend on some sort of Laplacian assumption to generate numbers where none exist. The Laplacian assumption is that when in a state of ignorance, the researcher should assign an equal probability to each possibility. The problems are well documented. However, there have been Bayesian proposals that at least somewhat circumvent the Laplacian assumption, and there might even be cases where there are strong grounds for assuming that the numbers really are there (see Fisher, 1973, for an example). Consequently, with respect to Bayesian procedures, we reserve the right to make case-by-case judgments, and thus Bayesian procedures are neither required nor banned from BASP.
OK – case-by-case analysis. That seems reasonable.
The journal editors are clear that their new policy does not mean they will accept less-than-rigorous research. They believe it will lead to more rigorous research:
However, BASP will require strong descriptive statistics, including effect sizes. We also encourage the presentation of frequency or distributional data when this is feasible. Finally, we encourage the use of larger sample sizes than is typical in much psychology research, because as the sample size increases, descriptive statistics become increasingly stable and sampling error is less of a problem.
Conclusion
I don’t know if the BASP solution to the problem of p-values is the best, ultimate, or only solution. Other solutions might include supplementing p-values with a discussion of the statistics that place them in their proper context, supplementing with Bayesian analysis, and having other requirements for scientific rigor. This would be a more difficult approach, and may not be able to dislodge the p-value from its lofty perch the way an outright ban might.
Requiring larger sample sizes is a good thing overall, but can create problems for young researchers just looking for a preliminary test of their new ideas. This then dovetails with another problem I and others have pointed out – presenting preliminary findings in the mainstream media as if they are definitive. Preliminary research is important, and if properly used can inform later research, but should not be used as a basis for clinical practice or hyperbolic headlines that ultimately misinform the public.
One solution is for journals to obviously separate preliminary research from confirmatory research. Preliminary research should be labeled as such with all the proper disclaimers and should not be the basis of hyped press releases. This may also provide the opportunity for having separate publishing rules for preliminary and confirmatory research – for example, for preliminary research journals can allow the use of p-values and techniques specifically designed to allow for smaller sample sizes.
The new BASP policy is a step in the right direction. At the very least I hope it raises awareness of the problems with relying on p-values and encourages a more nuanced understanding among researchers of statistics and methodological rigor.

